Savoir effectuer une division euclidienne
Objectifs pédagogiques
Manipuler et convertir des nombres en représentation binaire, hexadécimal et décimal
Introduction
En tant qu'être humain nous utilisons tous naturellement la base 10 pour représenter des nombres, c'est à dire qu'on fait usage des 10 chiffres (ou symboles) suivant : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Ex : "cent" = 100, "vingt" = 20, "quatorze" = 14, "un" = 1, etc.
Cela n'a rien de surprenant puisqu'on apprend à compter sur les dix doigts de la main et à écrire des nombres sous cette forme dès notre plus jeune âge !
On appelle ça le système de numération décimal (ou base 10).
Les ordinateurs eux utilisent un système différent du notre : le système de numération binaire (base 2) utilisant 2 symboles : le 0 et le 1 !
Il existe également le système de numération hexadécimal (base 16) qui fait usage de 16 symboles : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Nous allons commencer par étudier le système binaire et ensuite nous étudierons le système hexadécimal (base 16).
Système de numération binaire
Un ordinateur est une machine utilisant des circuits électriques et composants électroniques divers... Il manipule constamment de la donnée : des valeurs numériques représentées en binaire (base 2), soit des 0 et des 1.
Ces 0 et ces 1 d'un point de vue électrique indiquent lorsque la tension est basse ou haute (voltage bas ou voltage haut) ou lorsqu'un interrupteur est ouvert ou fermé, etc.
Ainsi l'ordinateur ne représente pas les nombres de la même manière que nous, par exemple, pour lui le nombre 9 est représenté par 1001 :
(9)_{10} = (1001)_{2}
Dans cet exemple, à gauche vous avez le nombre représenté en décimal (base 10) et à droite son équivalent en binaire (base 2).
D'une façon générale, lorsqu'on travaille avec des nombres en bases différentes on utilise la notation suivante :
(n)_p
où n représente le nombre et p la base.
Cela permet d'éviter toute confusion : on sait que le nombre 1001 (binaire) vaut neuf et non pas mille un !
Conversion d'un nombre entier vers un nombre en base p
Voyons comment convertir un nombre entier en base 10 vers un nombre en base p (binaire ou hexadécimal par ex). On va utiliser la méthode des divisions euclidiennes successives.
Est-ce que vous vous souvenez de vos cours de CM1/CM2 (vous deviez avoir environ 10 ou 11 ans) 🙃 ?
À cet âge on découvrait comment poser une division euclidienne :
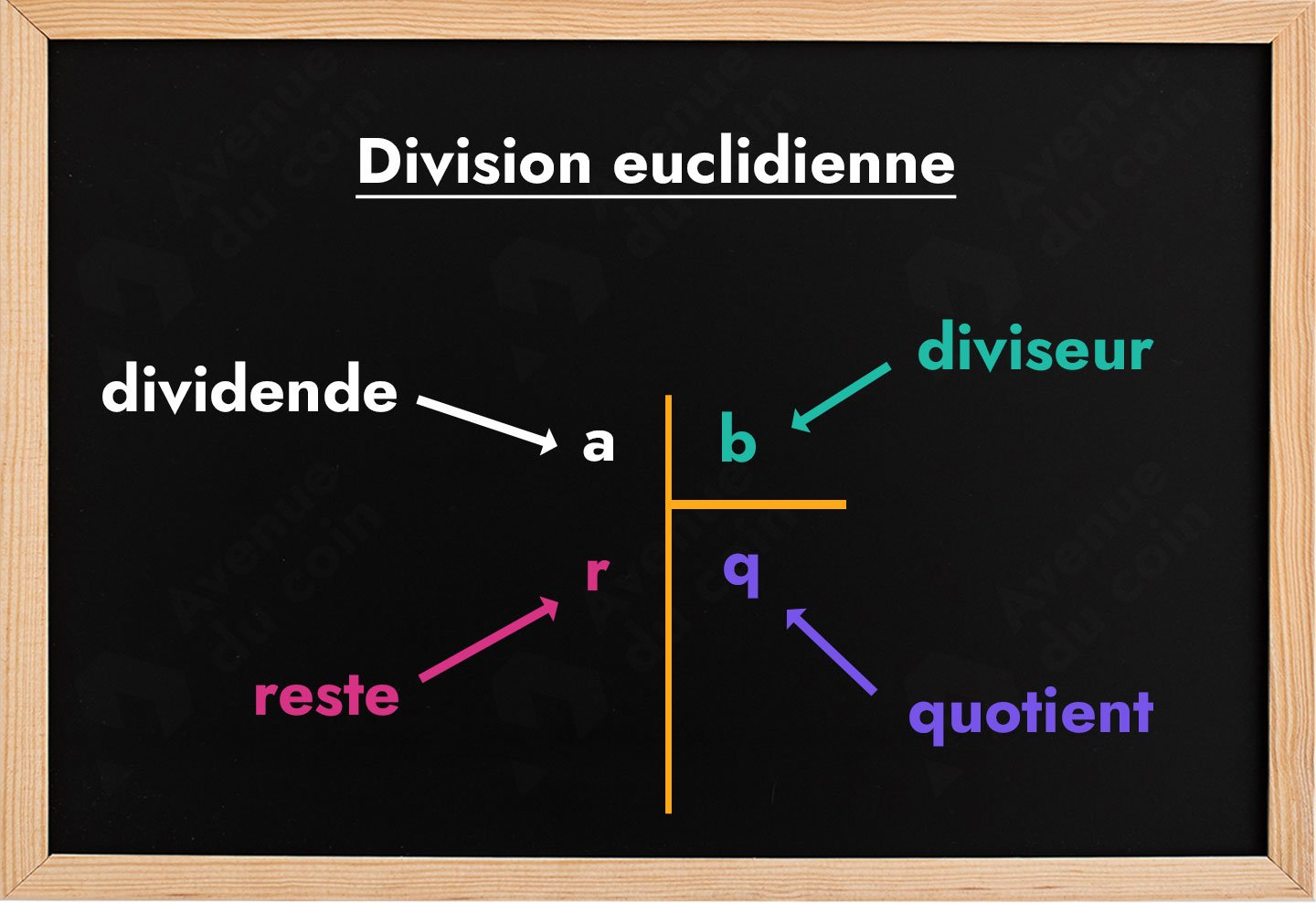
Eh bien nous allons de nouveau nous en servir !
Méthode des divisions euclidiennes successives
Pour convertir un nombre entier n en base p, il faut effectuer une division euclidienne de n par p et recommencer une division avec le quotient jusqu'à obtenir un quotient égal à 0.
Une fois l'opération terminée, il suffit de noter les restes des divisions successives dans l'ordre inverse (de la dernière division vers la première) pour obtenir la représentation du nombre en base p.
Numération des entiers (propriété)
Pour tout entier naturel p non nul appelé base, tout nombre entier naturel n peut se décomposer sous la forme suivante :
n = \displaystyle\sum_{i=0}^{k-1} a_{i} \times p^{i} \\\ \\\
(a_{k-1} a_{k-2} \ldots a_2a_1a_0)_p = a_{k-1} \times p^{k-1} + a_{k-2} \times p^{k-2} + \ldots + a_2 \times p^2 + a_1 \times p + a_0
Avec :
k représentant le nombre total de chiffres
p \geq 2
et les coefficients a_{i} (appelés chiffres) vérifiant la condition suivante :
0 \leq a_{i} \leq p - 1
et :
a_{k-1} \ne 0
Conversion d'un nombre entier en binaire (base 2)
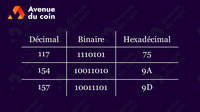
Appliquons la méthode des divisions euclidiennes successives sur le nombre 117 :
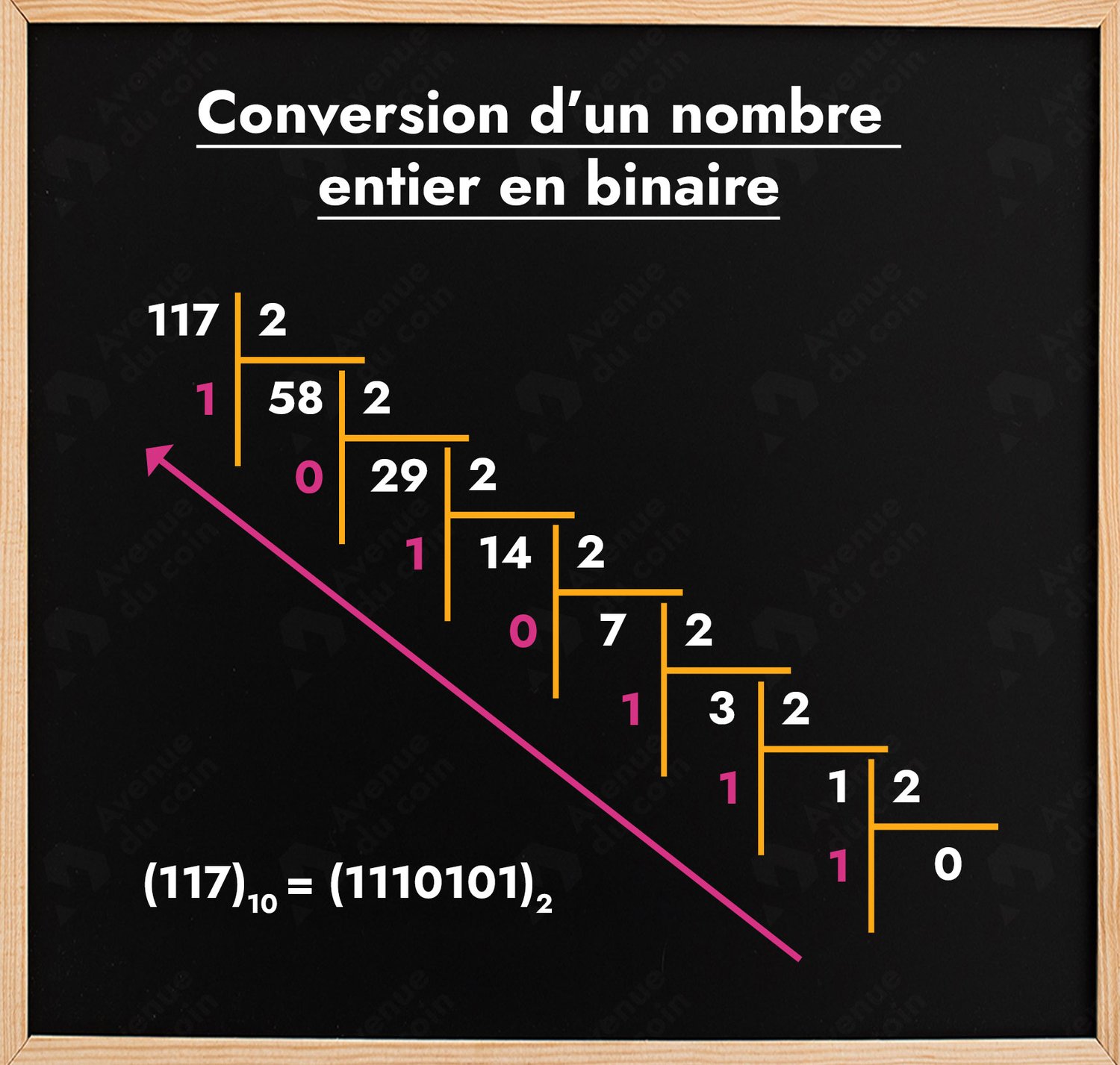
Comme expliqué : une fois que le quotient est de 0, on s'arrête et il suffit d'inscrire les restes dans le sens de la flèche pour obtenir la représentation en binaire.
On obtient bien 1110101.
On peut facilement re-convertir 1110101 en base 10 en se fondant sur la définition vu précédemment :
On lit le nombre binaire de la droite vers la gauche, chiffre par chiffre. Le premier chiffre (en partant de la droite) est multiplié par 2 puissance 0, le second par 2 puissance 1, puis le troisième par 2 puissance 2 et ainsi de suite...
(117)_{10} = (1110101)_{2}
(117)_{10} = 1 \times 2^6 + 1 \times 2^5 + 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0
(117)_{10} = 64 + 32 + 16 + 0 + 4 + 0 + 1
Conversion d'un nombre entier en hexadécimal (base 16)
Faisons cet exercice avec le nombre 27899 :
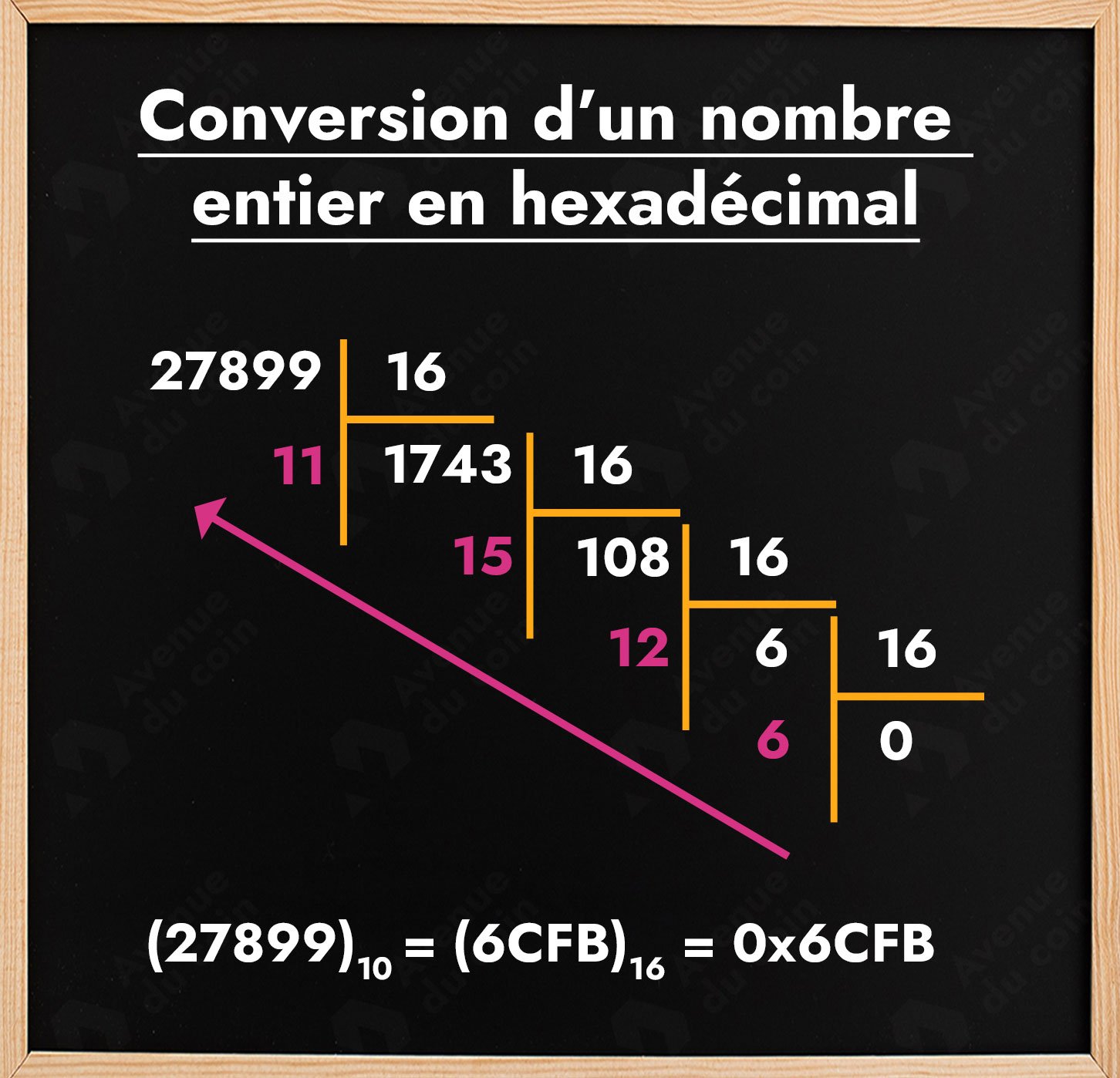
C'est le même principe (division successives par la base p) sauf qu'à la fin on remplace les restes compris entre 10 et 15 par une lettre (leur représentation hexadécimal).
Dans l'exemple on a remplacé 12 par C, 15 par F et 11 par B.
Car souvenez-vous, la base 16 utilise les 16 symboles suivant : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Le nombre 27899 s'écrit 6CFB en hexadécimal. Il existe une représentation alternative, il suffit d'ajouter le préfixe 0x (zéro x), ce qui donne : 0x6CFB.
(27899)_{10} = (6CFB)_{16}
(27899)_{10} = 6 \times 16^3 + 12 \times 16^2 + 15 \times 16^1 + 11 \times 16^0
(27899)_{10} = 24576 + 3072 + 240 + 11
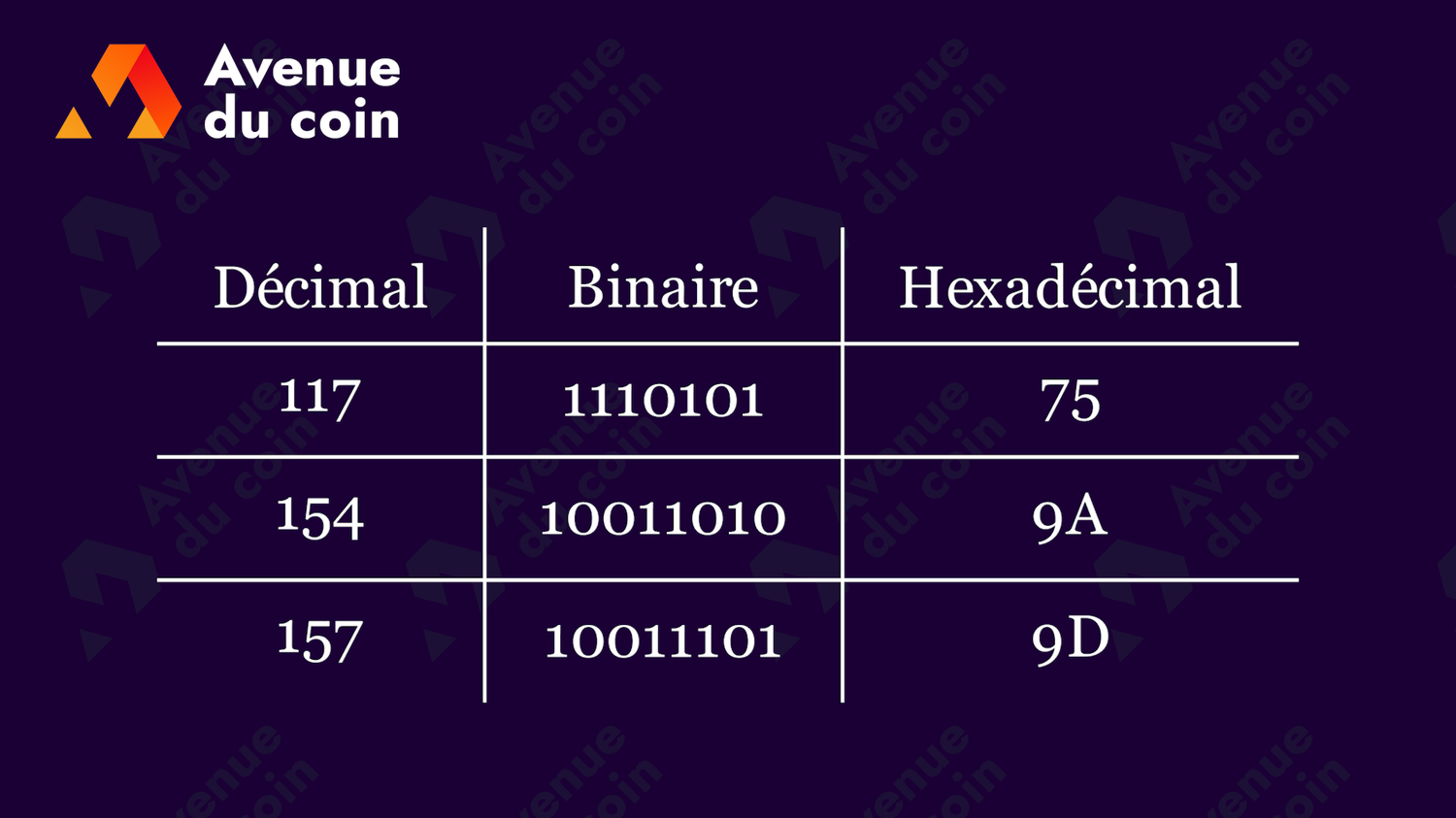
Tableau de conversion (décimal, binaire, hexadécimal)
Voici un tableau de conversion des nombres allant de 0 à 15 (décimal) vers les bases binaire et hexadécimal :
| Décimal | Binaire | Hexadécimal |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| Décimal | Binaire | Hexadécimal |
|---|---|---|
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Ce tableau va nous être utile pour la section suivante.
Convertir facilement un nombre binaire en hexadécimal et inversement
On peut facilement passer d'un nombre binaire vers un nombre hexadécimal et vice-versa en s'aidant du tableau de conversion précédent.
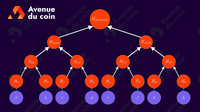
Pour cela on vient lire le nombre binaire de la droite vers la gauche en se déplaçant de 4 en 4 et on va former des paquets de 4 chiffres (quartet), si le dernier paquet possède moins de 4 chiffres, alors on rajoute autant de 0 que nécessaire.
Une fois que nous avons nos paquets de 4 chiffres binaires, on peut en déduire la représentation hexadécimal grâce au tableau de conversion.
Exemple de conversion
Voici un exemple avec le nombre (111100101001100)_{2} :
On a pu convertir facilement (111100101001100)_{2} en hexadécimal : 0x794C.
Notez qu'on a rajouté un 0 tout à gauche (sur le schéma) pour former le dernier paquet de 4 comme expliqué précédemment.
Bibliographie
[1] A. Cazes and J. Delacroix, Architecture des machines et des systèmes informatiques, 6 ed. Dunod, 2018.
[2] X. Chanet and P. Vert, Mathématiques pour l’informatique – Pour le BTS SIO, 3 ed. Dunod, 2021.
[3] S. Pasquet, “Nombre de chiffres d’un nombre,” Mar. 2019, [Online]. Available: https://www.mathweb.fr
