Dans cet article nous allons voir à quoi servent les arbres de Merkle et comment ils sont utilisés dans la blockchain.
Ce cours existe également au format vidéo : https://youtu.be/o_EhMMWKteI
Prérequis
- Savoir expliquer le principe de fonctionnement d'une fonction de hachage
Objectifs pédagogiques
- Illustrer un arbre de Merkle et ses différents éléments
- Donner l'exemple d'une Merkle Proof d'une donnée de l'arbre
- Comprendre comment la Merkle Proof est utilisée et dans quel but
- Expliquer en quoi un arbre de Merkle peut être utile pour une collection de NFT
Introduction
L'arbre de Merkle également connu sous le nom de Merkle Tree (en anglais), est une structure de données qui a été inventée en 1979 par Ralph C. Merkle, un célèbre cryptographe américain et chercheur en nanotechnologies.
Un des avantages de cette structure est d'offrir la possibilité de vérifier l'intégrité d'un ensemble de données sans avoir besoin de toutes les connaitre au moment de la vérification.
Cas d'usages
Les cas d'usages sont nombreux, en voici deux :
Les light nodes Bitcoin utilisent les arbres de Merkle afin de ne pas avoir à stocker toutes les transactions tout en gardant la possibilité de vérifier les paiements [2], ce qui permet d'alléger la quantité de données à télécharger pour se synchroniser à la blockchain et donc d'économiser de l'espace disque.
Les collections de NFT font souvent usage des Merkle Trees pour construire une whitelist. Cela leur permet d'éviter d'avoir à stocker l'intégralité des adresses directement dans le smart-contract : sur des blockchains comme Ethereum, ça serait très couteux en frais de gas.
Les éléments d'un Merkle Tree
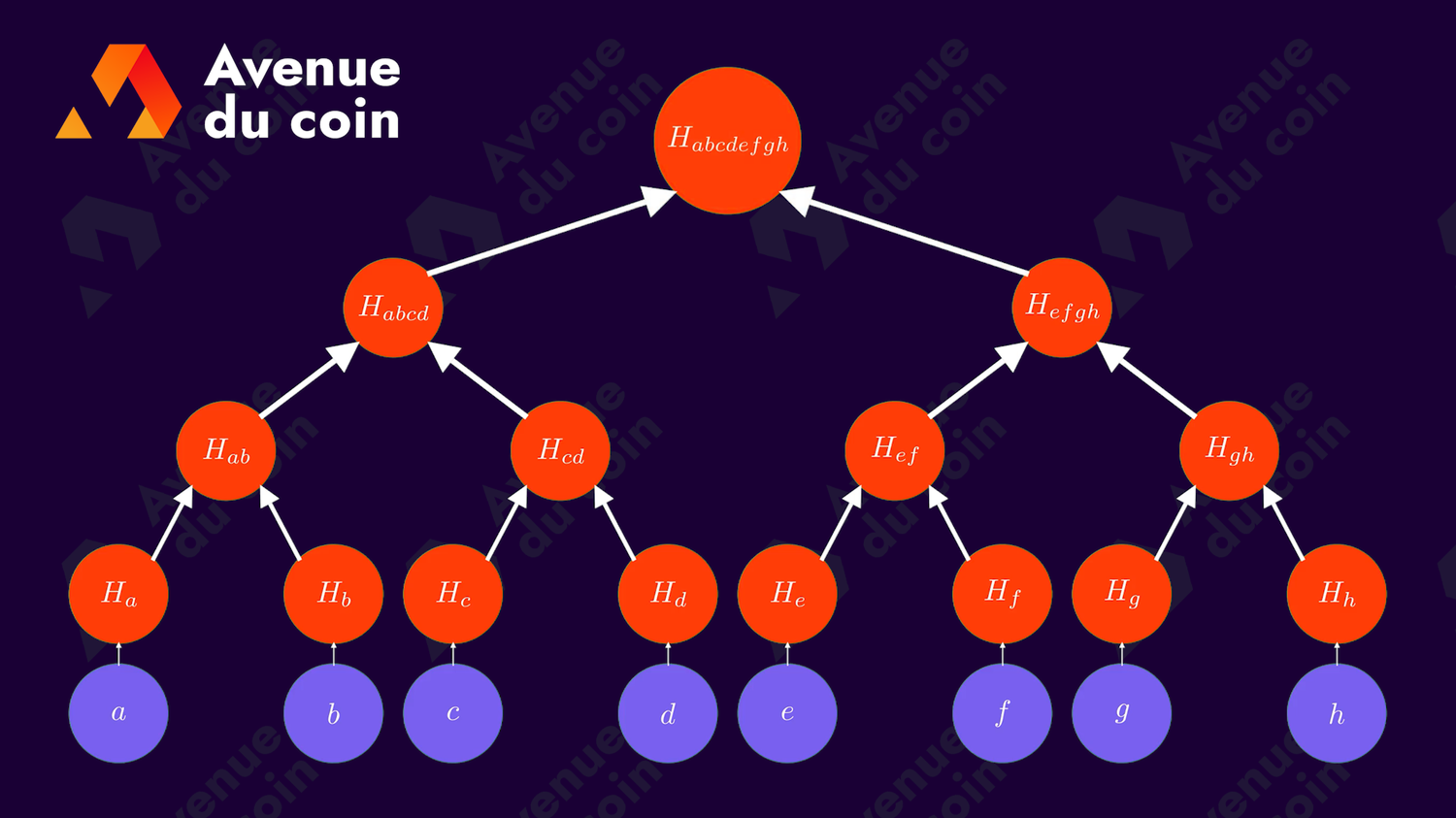
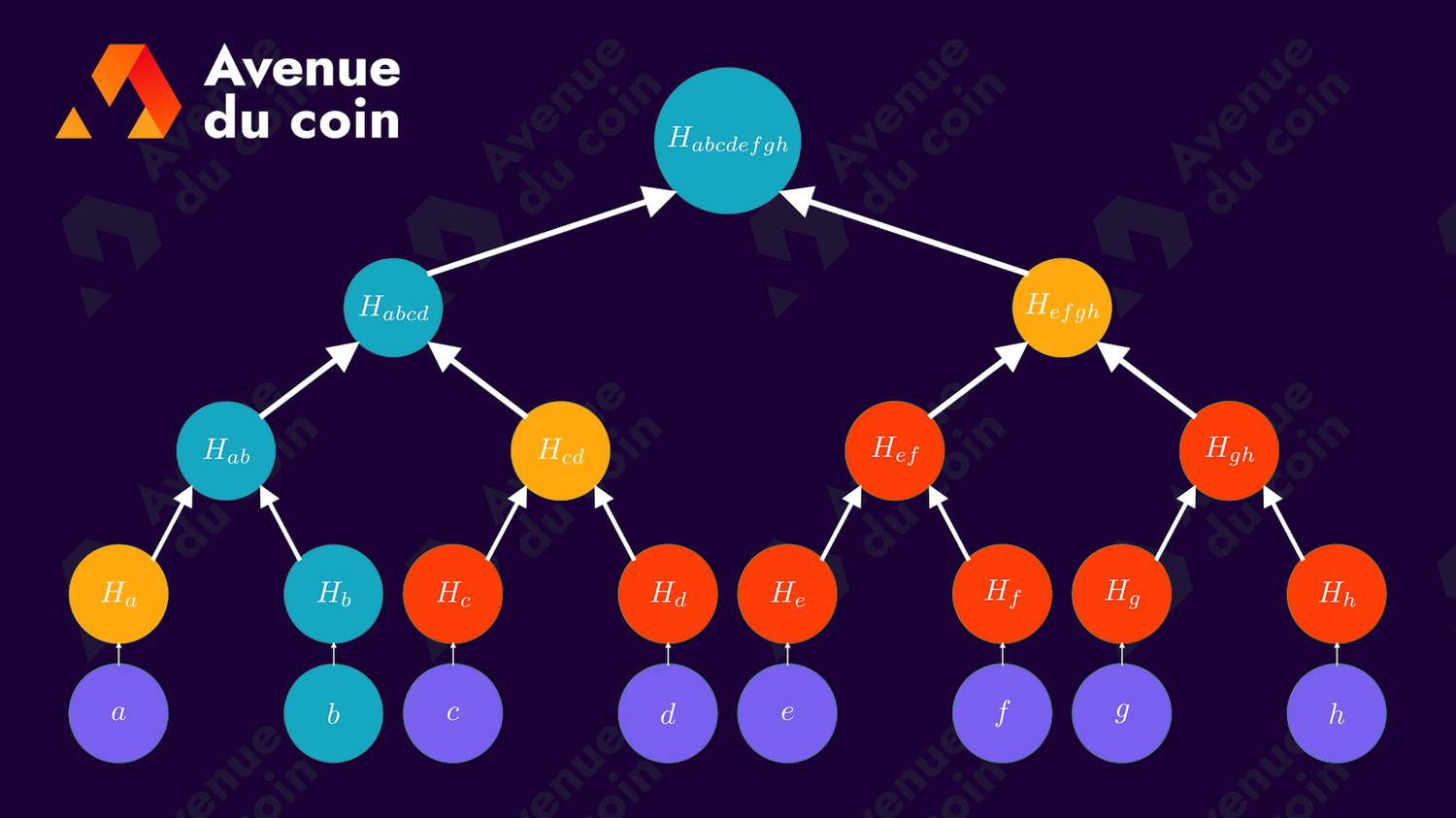
Un arbre de Merkle est construit à partir d'éléments de base appelés noeuds, chaque noeud est un hash.
Sur le schéma ci-dessous, les noeuds sont les cercles orange.
Niveaux
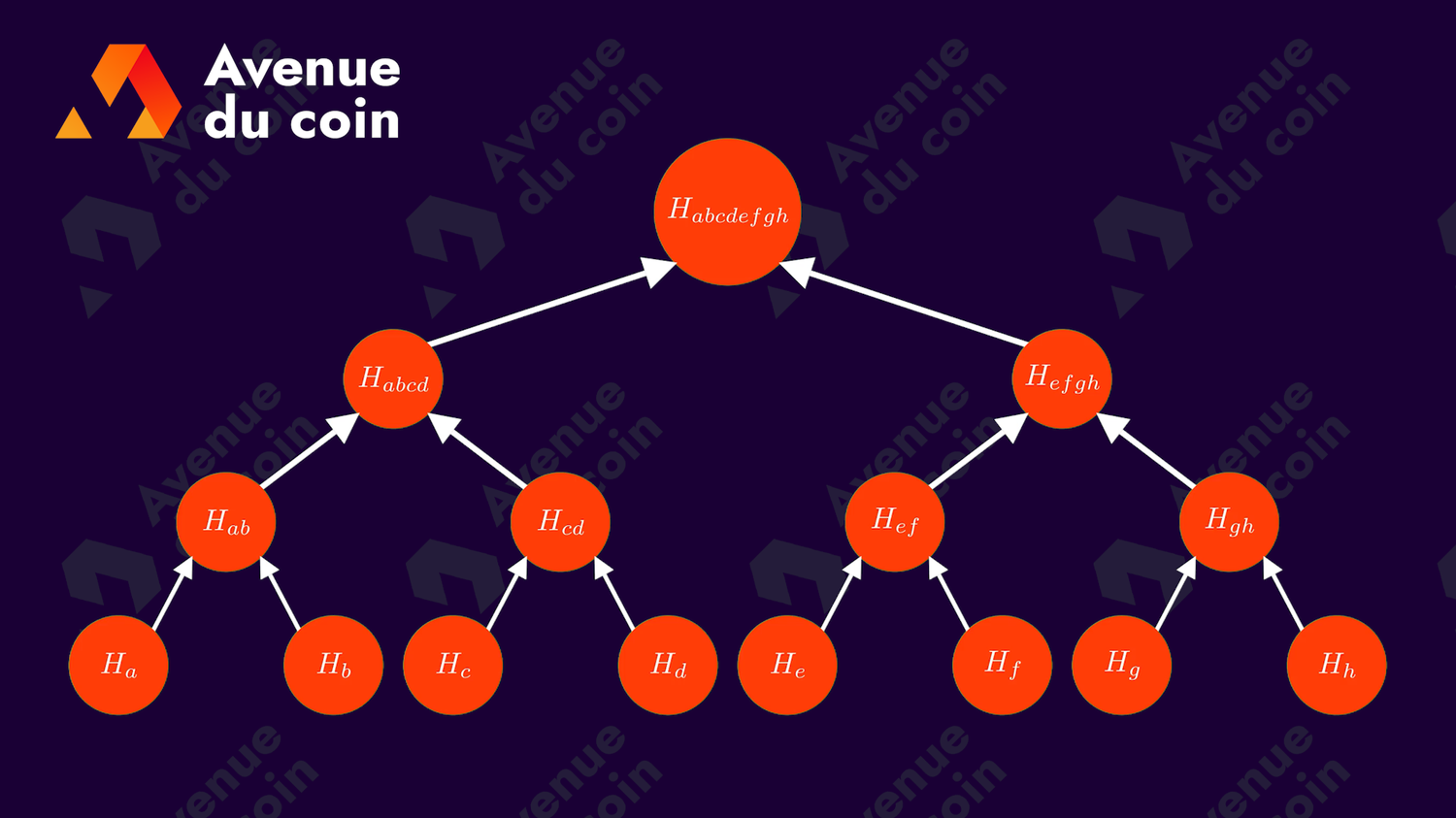
On peut distinguer plusieurs niveaux dans un arbre, par convention on commence au niveau 0 tout en haut, soit la racine de l'arbre.
Puis quand on descend, on passe au niveau 1, puis 2, puis 3, etc.
Un noeud est donc placé à un certain niveau, on parle également de pronfondeur d'un noeud.
Pour calculer le niveau d'un noeud, on mesure la longueur du chemin reliant la racine à ce noeud.
La hauteur de l'arbre est égale à l'indice du noeud le plus profond (ou niveau max).
Racine de Merkle
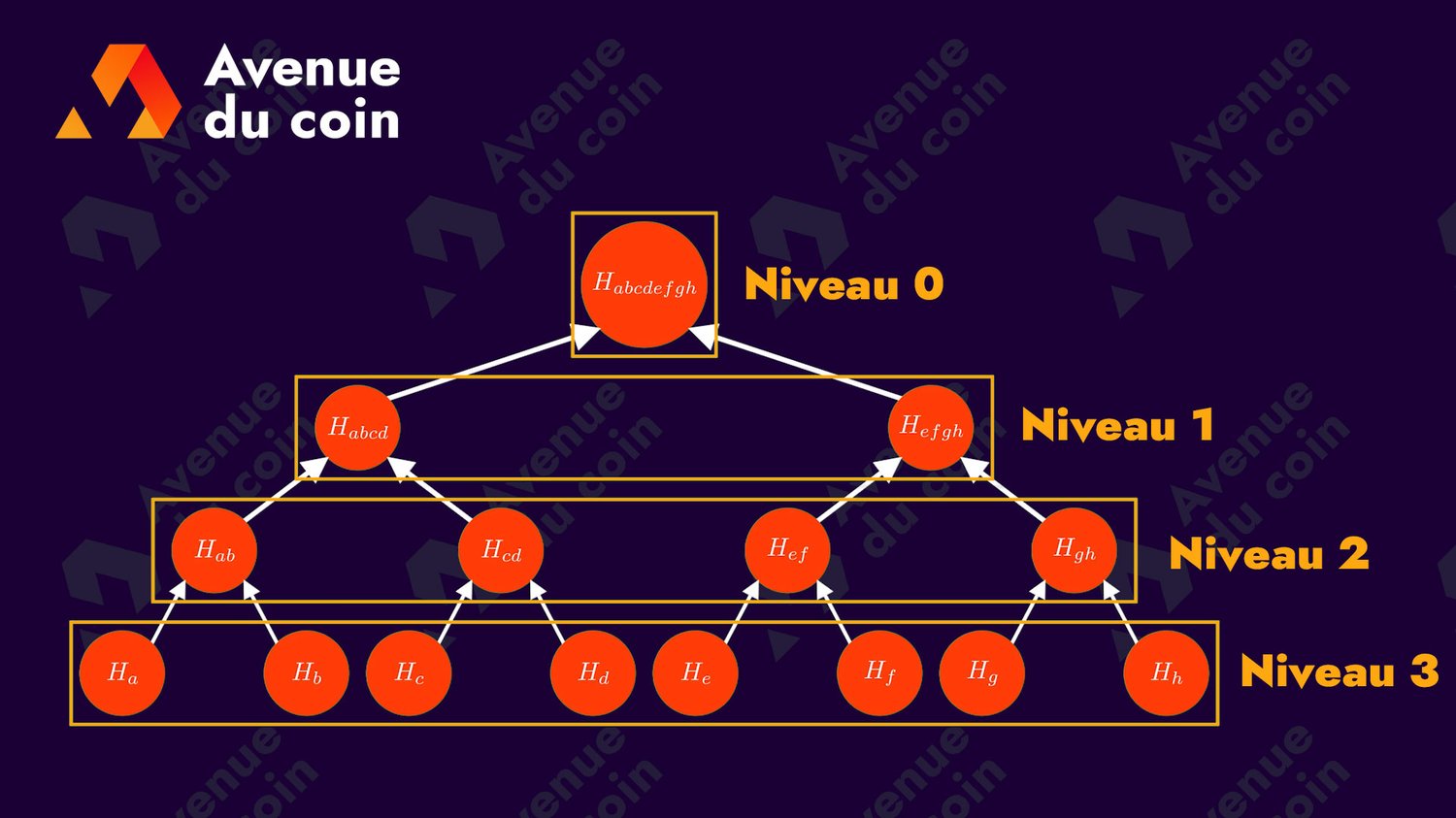
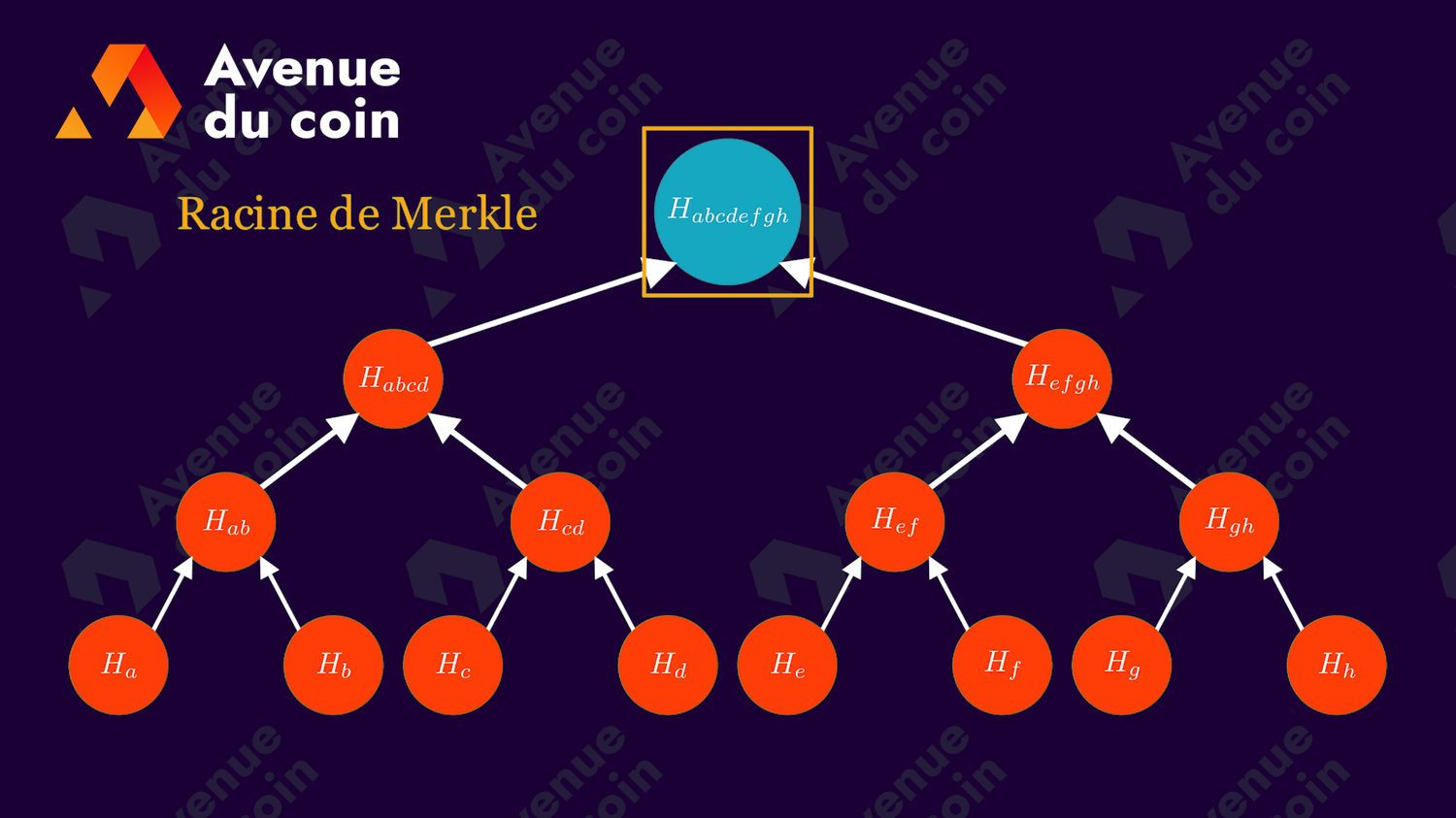
La racine de Merkle (Merkle root en anglais) est le seul noeud qui n'a pas de parent, c'est celui situé tout en haut de l'arbre (niveau 0).
Noeud parent
Un noeud possède un parent (sauf la racine).
Noeuds enfants
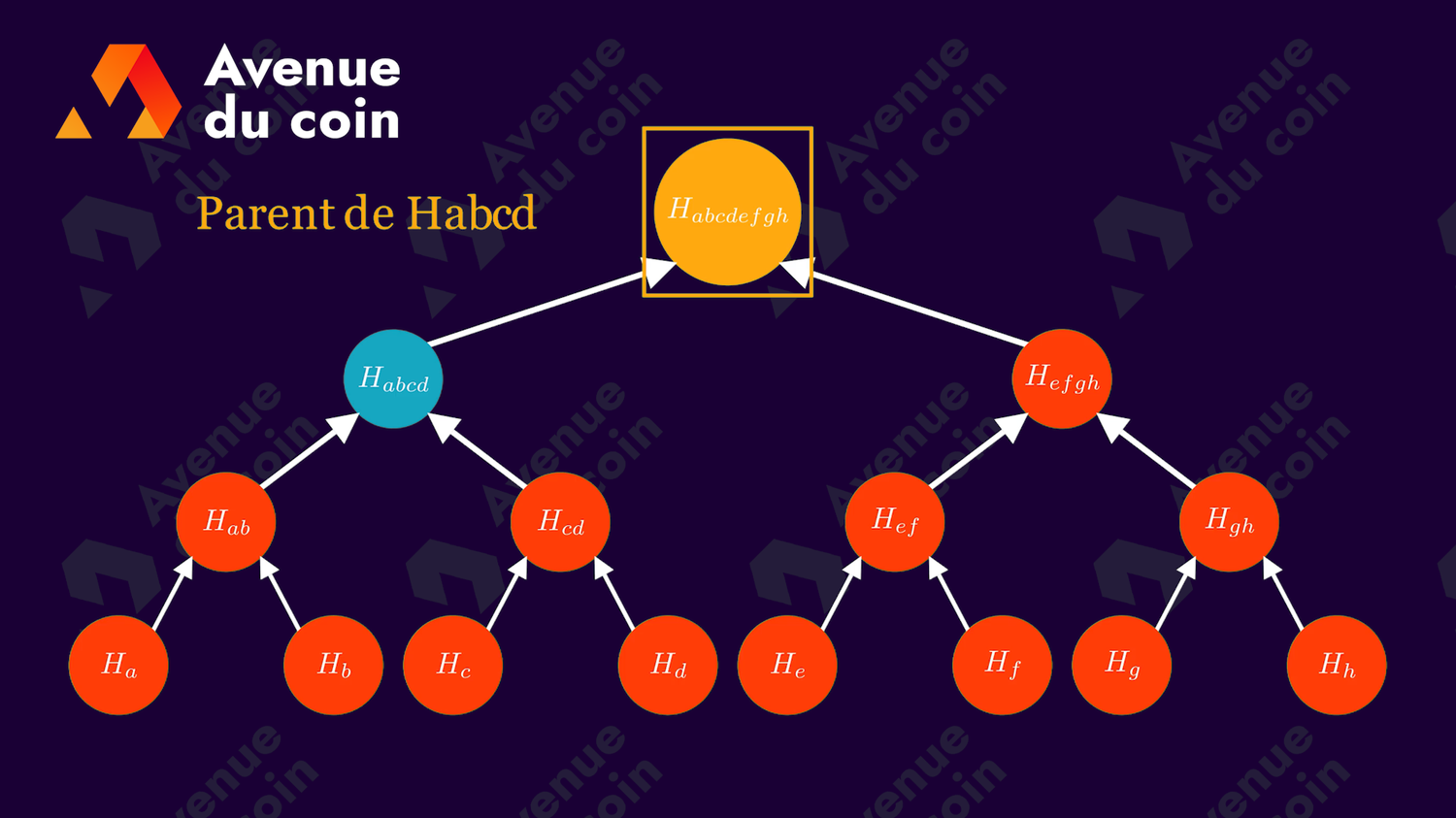
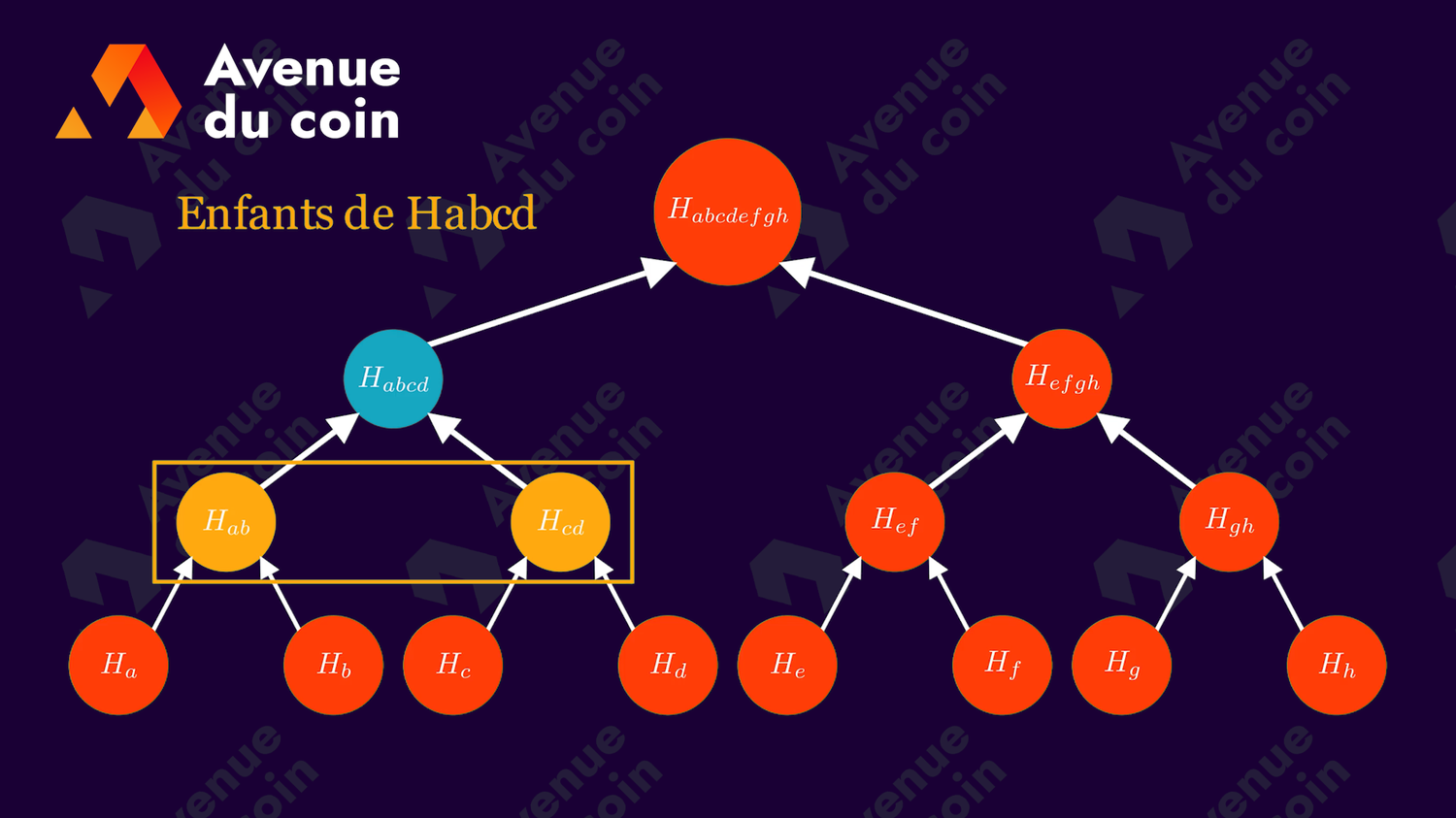
Un noeud peut avoir des enfants, au maximum 2*.
*sans rentrer dans les détails, dans cet article nous utilisons un binary Merkle Tree, mais il peut y avoir d'autres variantes (K-ary) ayant un nombre d'enfants par noeud plus élevé.
Feuilles
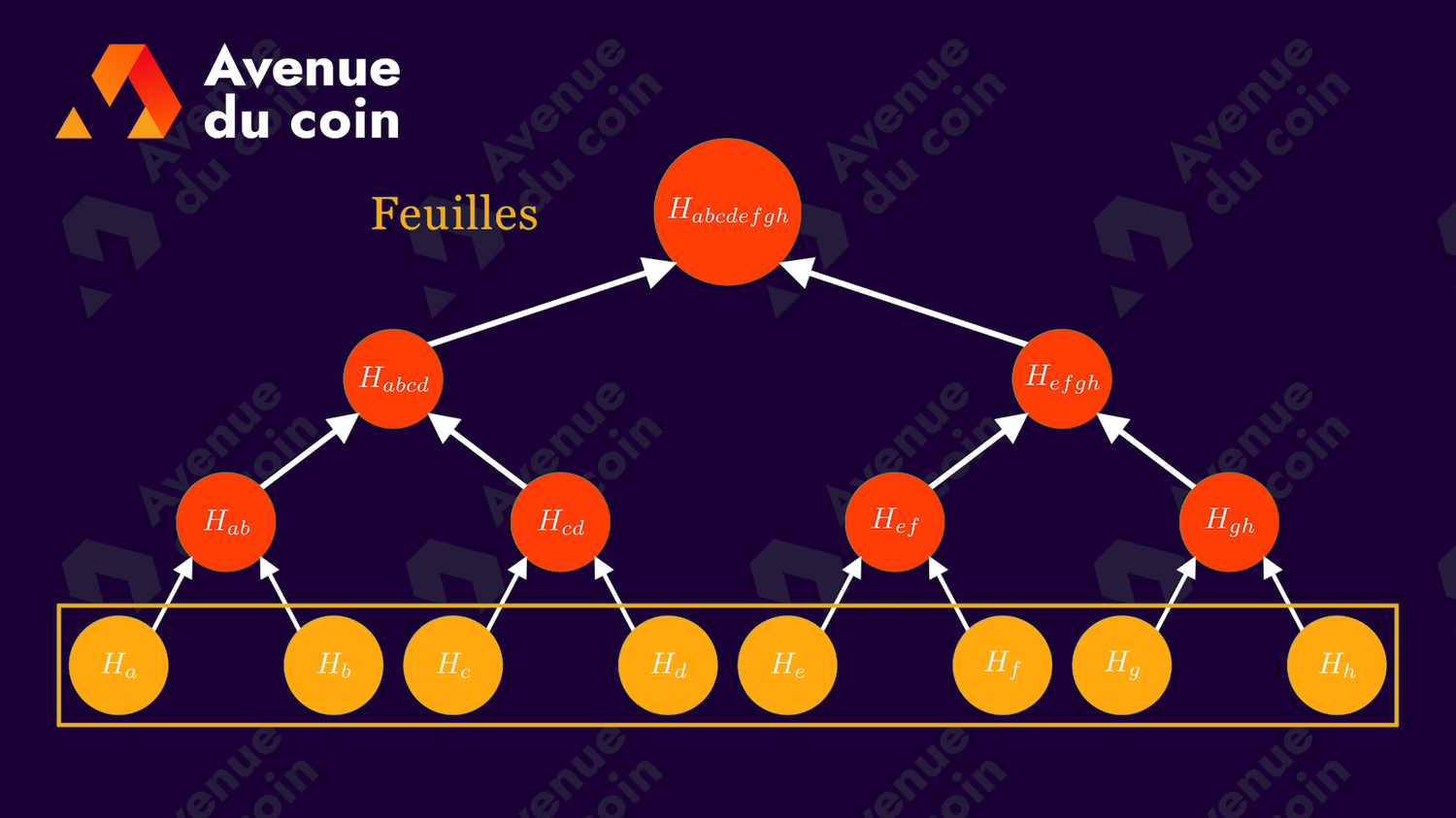
Un noeud n'ayant aucun enfant est une feuille (leaf).
Construction d'un Arbre de Merkle
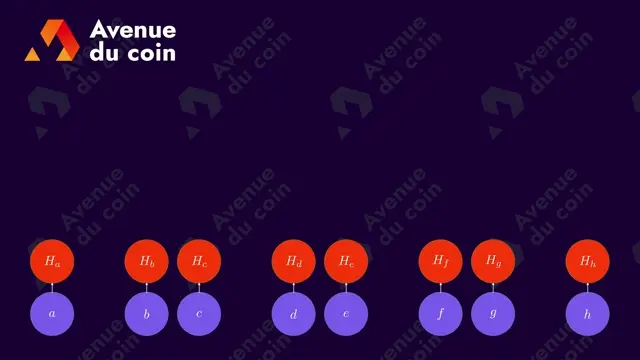
Un arbre de Merkle se construit de bas en haut. Pour obtenir la base de l'arbre il faut d'abord un ensemble de données : une liste d'adresses publiques ou une liste de transactions par exemple.
Feuilles
On commence par hasher les données pour former les feuilles de l'arbre.
Sur l'animation suivante les données sont représentées en violet.
Noeuds parents
Une fois les feuilles de l'arbre construites, il faut construire les noeuds parents. Pour obtenir un parent, on fait un hash de la concaténation de deux noeuds enfants.
Rappel : la concaténation est le fait de mettre bout à bout au moins deux chaînes de caractères.
\text{Exemple 1 : } \\\ \\\
a = "hello" \\\
b = "world" \\\ \\\
\text{Concaténation de a et b :} \\\ \\\
a \mathbin\Vert b = "helloworld" \\\ \\\
\text{Exemple 2 : } \\\ \\\
H_a = "d81a65..." \\\
H_b = "3b64db..." \\\
H_a \mathbin\Vert H_b = "d81a65...3b64db..."
Imaginons un ensemble E contenant les feuilles de l'arbre :
E = \{H_a, H_b, H_c, H_d, H_e, H_f, H_g, H_h\}
On peut construire le noeud parent H_{ab} avec les deux enfants : H_a et H_b
H_{ab} = hash(H_a \mathbin\Vert H_b)
On hash les noeuds deux par deux et on répète l'opération à tous les niveaux jusqu'à obtenir la racine de Merkle.
L'exemple fonctionne très bien car le nombre d'élément de départ (8) est une puissance de 2 !
2 ^3 = 8
Il est donc logique qu'on puisse diviser par 2 le nombre d'éléments à chaque fois qu'on remonte d'un niveau.
Voici un arrêt sur image de l'arbre final :
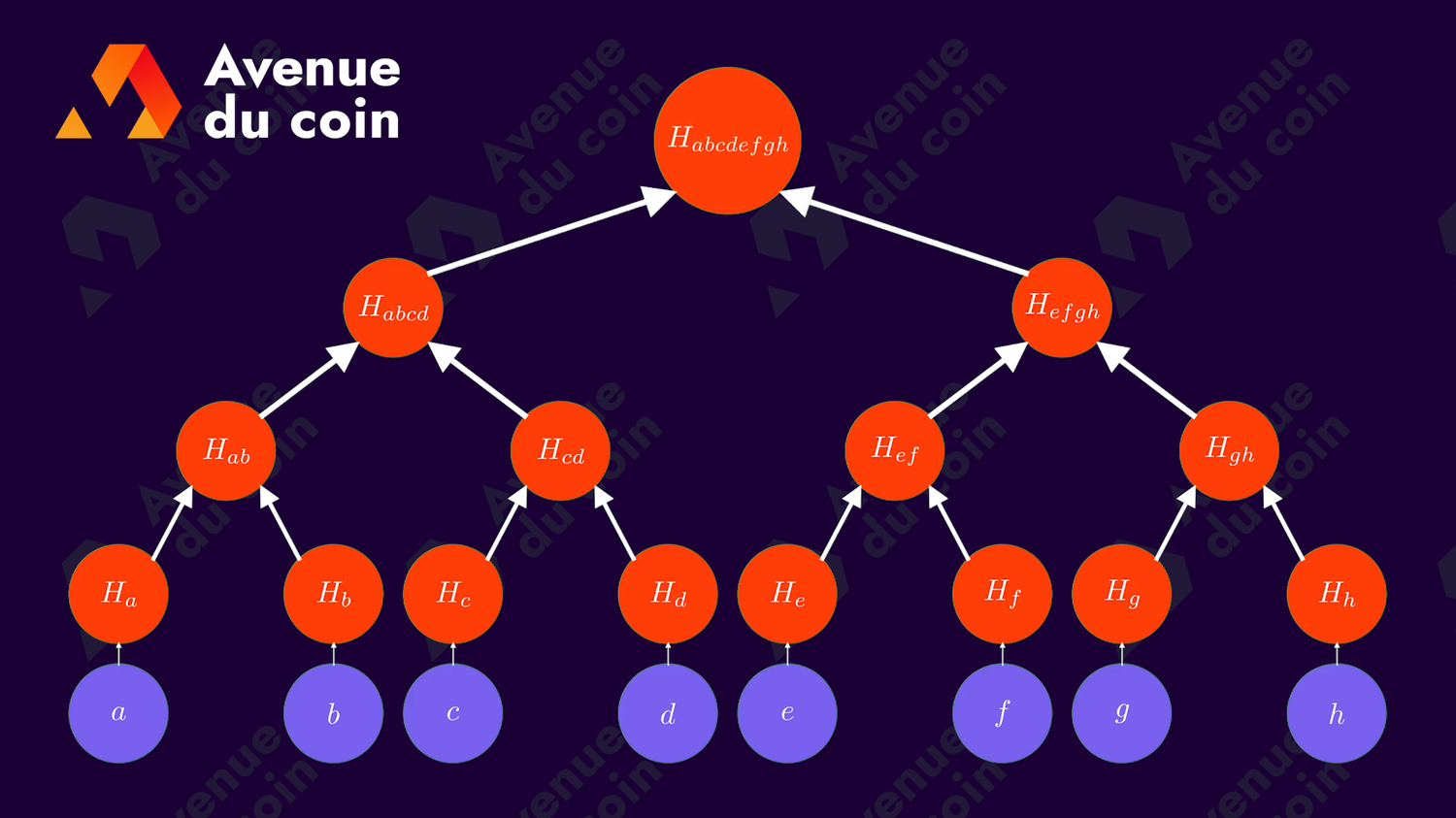
Veuillez noter que les données initiales (cercles violet) ne font pas partie de l'arbre de Merkle.
Nous avons choisi de les représenter uniquement pour faciliter la compréhension et la visualisation.
Cas particuliers
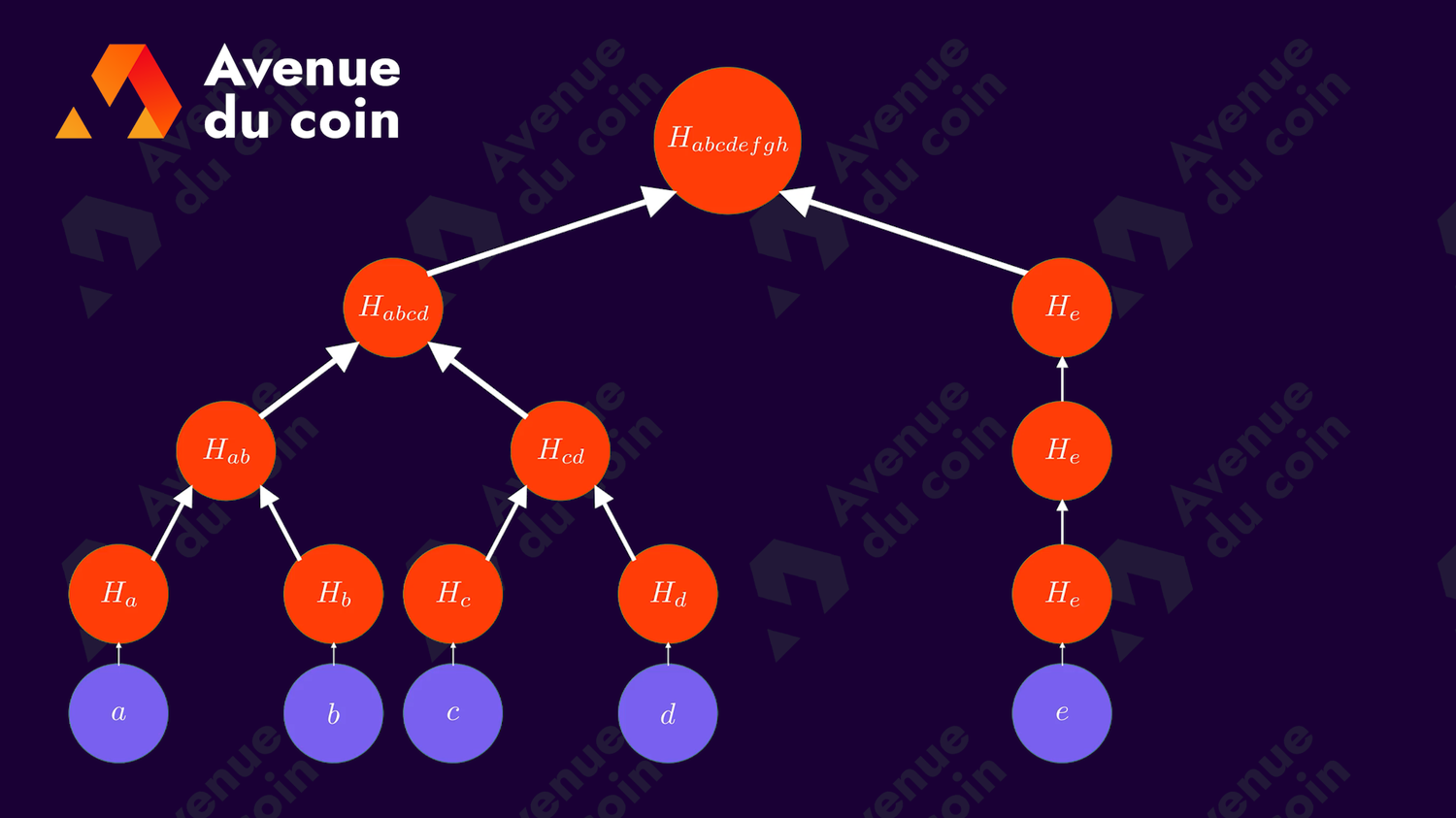
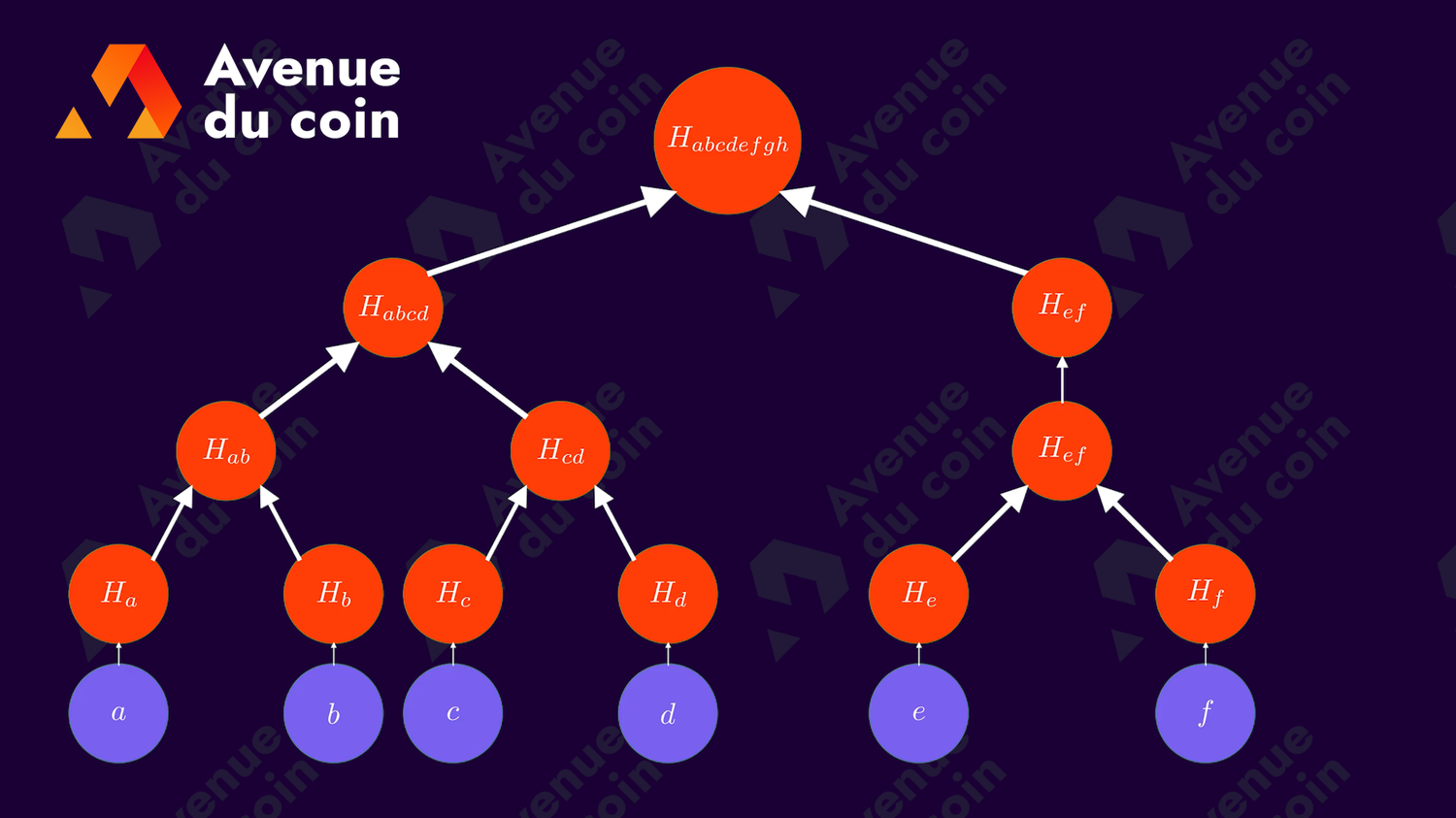
Comme le nombre d'élément de départ n'est pas toujours une puissance de 2, au bout d'un moment un noeud va se retrouver sans frère pour former le parent.
Il existe plusieurs solutions pour corriger ce problème, pour en citer quelques unes : on peut remonter le noeud qui n'a pas de frère ou le dupliquer.
L'important est de rester consistant (utiliser la même solution) entre les différentes entités (serveurs, utilisateurs, applications...)
Voici quelques exemples (en remontant le noeud) :
Merkle Proof
La Merkle Proof ou preuve de Merkle permet à une entité (serveur, application, etc.) détenant un arbre de Merkle complet, de prouver à une deuxième entité ne possédant que la racine, qu'un élément fait partie de l'arbre.
Sur le schéma ci-dessous, on voit un serveur à gauche qui détient l'arbre complet et un deuxième serveur à droite qui détient uniquement la racine de Merkle. Ils ont tous les deux la même racine.
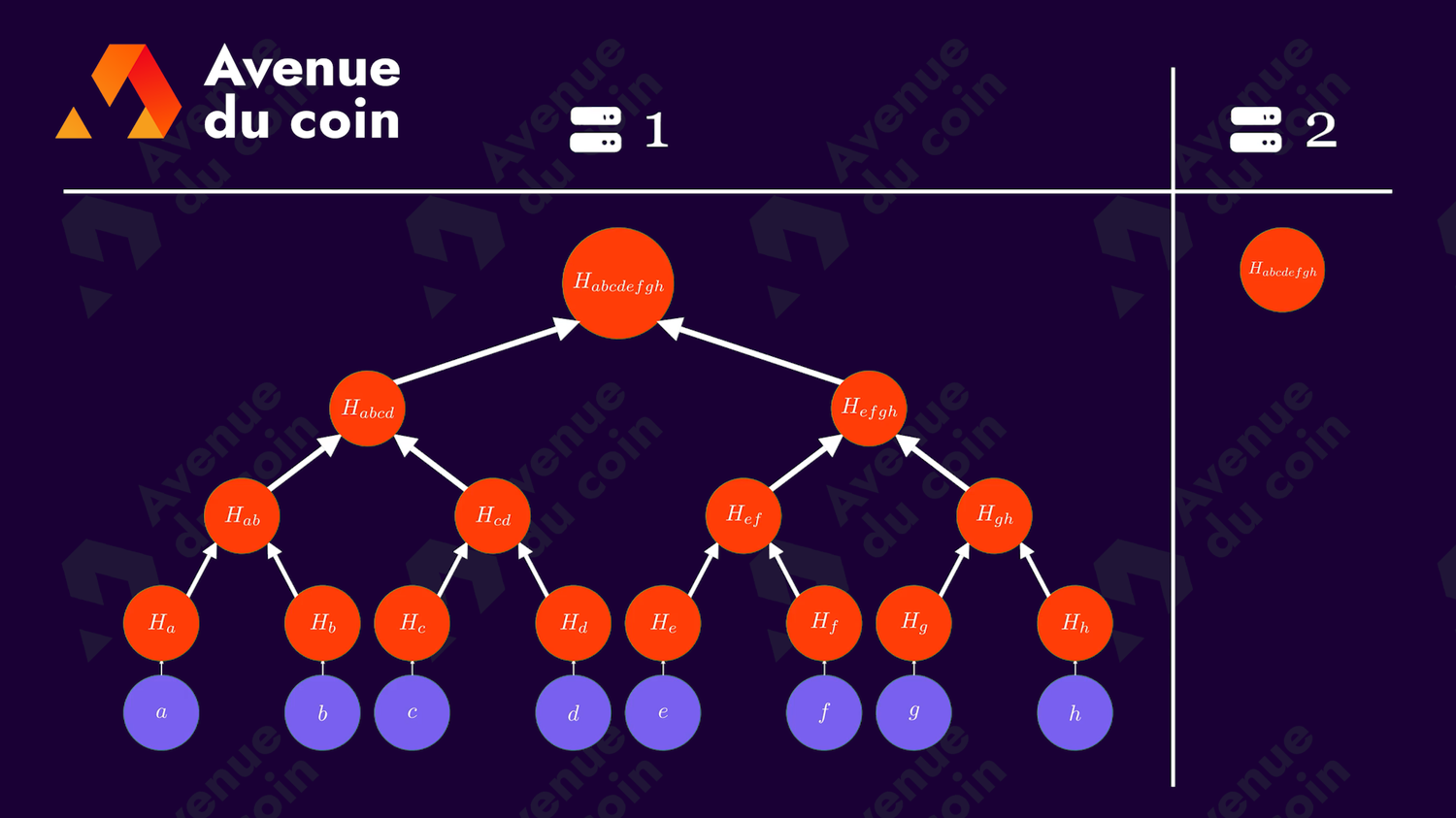
Grâce à la Merkle Proof, le 2e serveur stockant uniquement la racine est en mesure de vérifier qu'un élément fait partie de l'arbre !
Nous allons voir comment ça fonctionne.
Constuction de la Merkle Proof
Pour construire la Merkle Proof, il faut posséder l'arbre complet (ou avoir au moins connaissance des données initiales et de connaître les règles de construction).
Si le 1er serveur (de l'illustration précédente) souhaite prouver au 2e serveur qu'un élément est dans l'arbre, il va devoir rassembler des informations : des noeuds spécifiques et leur position (gauche ou droite).
Par exemple :
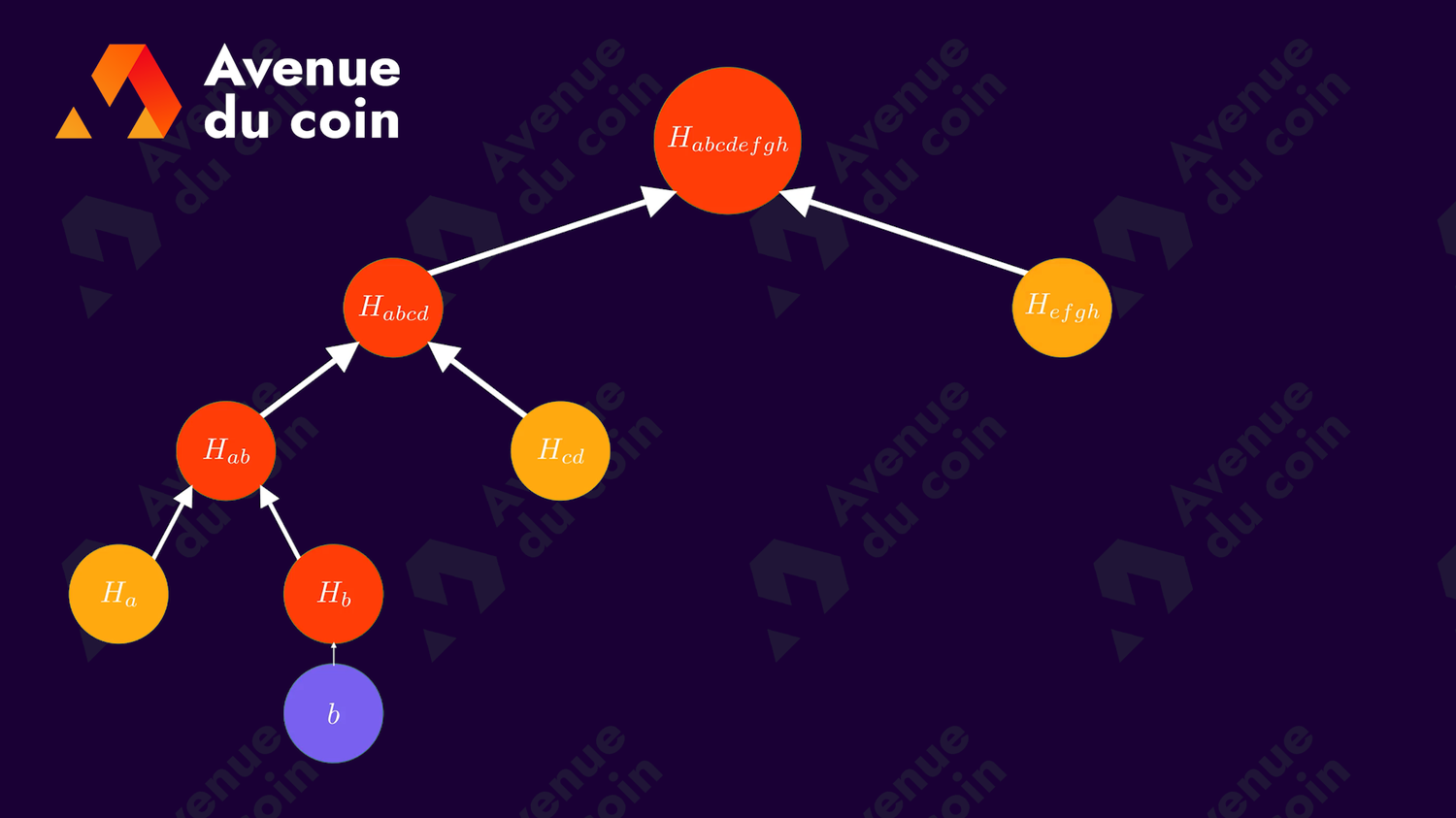
Si on souhaite prouver que b (le deuxième cercle violet en partant de la gauche) est dans l'arbre, on a besoin de quelques noeuds pour former la preuve de Merkle.
L'idée est de partir de b et de remonter jusqu'à la racine de Merkle en prenant note de chaque noeud frère nécessaire à la création du noeud parent (pour monter d'un niveau).
Voici une illustration pour cet exemple :
En suivant le chemin (noeuds verts) on remarque que nous avons seulement besoin des noeuds en jaune pour remonter jusqu'à la racine de Merkle en partant de b :
\{H_a, H_{cd}, H_{efgh}\}
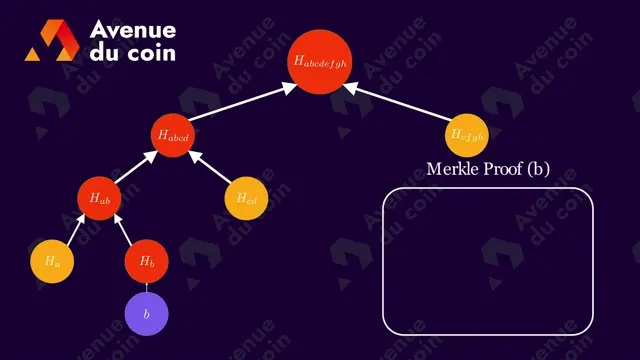
En masquant les noeuds dont nous n'avons pas besoin, on y voit un peu plus clair :
La Merkle Proof de b est l'ensemble des noeuds en jaune dans l'ordre du noeud le plus profond au moins profond (du plus bas vers le plus haut sur le schéma).
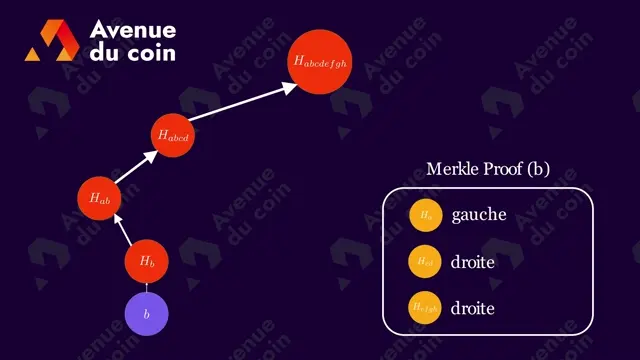
Il faut également indiquer si le noeud est à gauche ou à droite :
H_a \rightarrow \text{gauche} \\\
H_{cd} \rightarrow \text{droite} \\\
H_{efgh} \rightarrow \text{droite}
Vérification de la Merkle Proof
Une fois en possession de la Merkle Proof, le 1er serveur peut l'envoyer au 2e.
Ce 2e serveur va hasher b puis utiliser les noeuds de la Merkle Proof jusqu'à obtenir une racine de Merkle.
Si la racine obtenue est la même que celle qu'il a stocké en mémoire, alors cela signifie que b fait bien partie de l'arbre.
Schéma d'usage concret
Pour terminer ce cours sur les arbres de Merkle, voyons ensemble un schéma un peu plus concret.
Imaginez une collection de NFT qui souhaite organiser une presale pour les membres de leur whitelist (une liste d'adresses autorisées à mint).
Au lieu de stocker l'intégralité des adresses directement dans le smart-contract, on peut utiliser un arbre de Merkle pour économiser des frais de gas !
L'idée est de construire un Merkle Tree à partir de la liste d'adresses de la whitelist et le stocker en dehors du contrat. Le smart-contract lui ne possèdera que la racine.
Déroulement du mint
- On peut imaginer qu'un utilisateur clique sur un bouton pour minter un NFT. Le site web va créer une preuve de Merkle pour cet utilisateur (s'il fait bien partie de la whitelist, sinon il va probablement afficher une erreur et dans le cas contraire, la preuve créée ne serait pas valide).
- Le site web va appeler le smart-contract avec la preuve de Merkle, le contrat pourra vérifier cette preuve et ainsi autoriser ou refuser le mint.
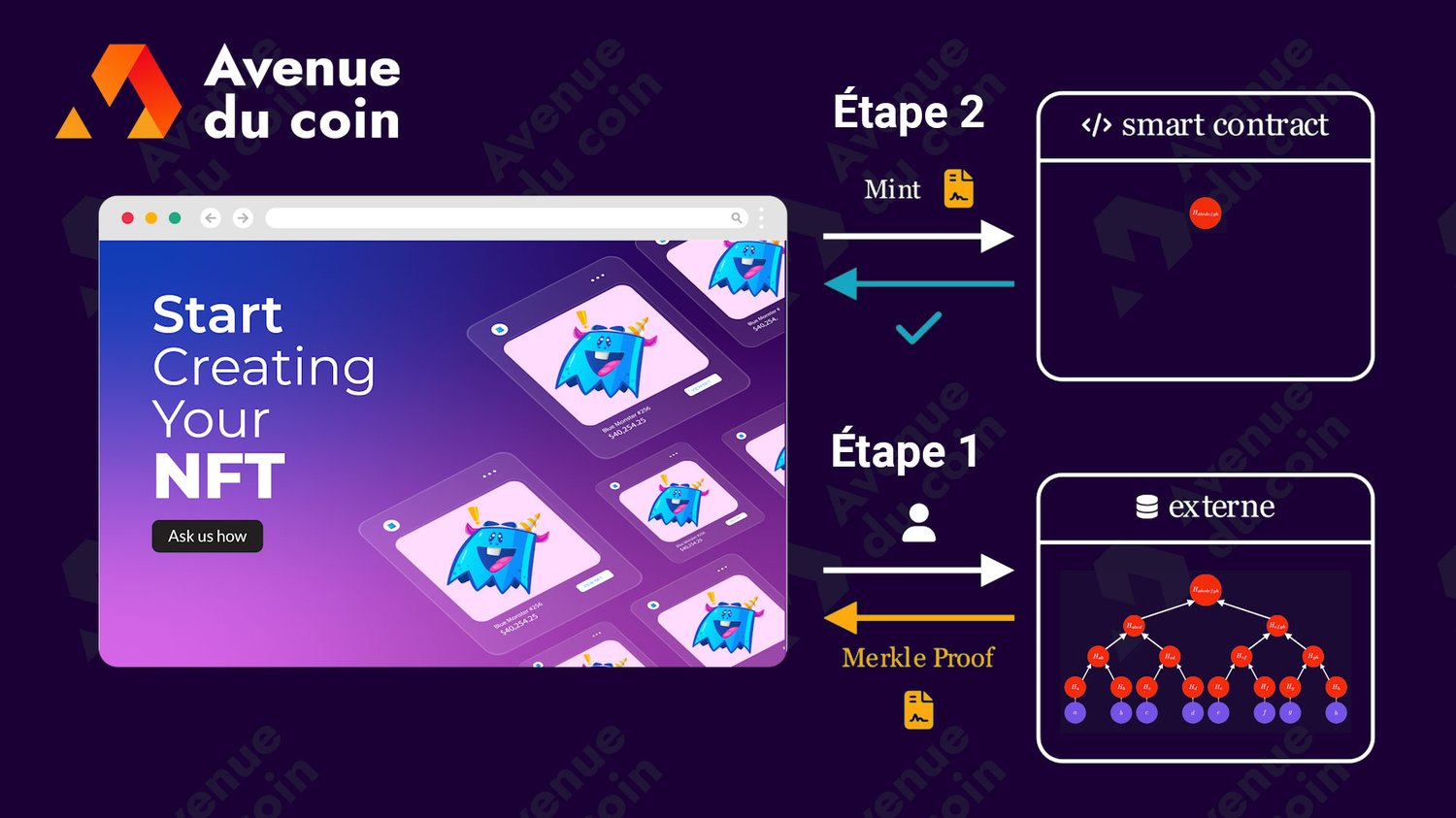
Ce qui est important à retenir, c'est que c'est le smart-contract qui va hasher lui-même l'adresse de l'utilisateur (hash de msg.sender en Solidity).
Par principe de sécurité, on ne fait pas confiance à ce que l'utilisateur nous envoie ! Sinon ça serait trop facile de se faire passer pour quelqu'un d'autre (un membre de la whitelist par exemple).
On peut en revanche utiliser la Merkle Proof sans problèmes (bien que ça soit l'utilisateur qui l'envoie), puisque si l'utilisateur n'est pas dans l'arbre, il ne peut pas créer une Merkle Proof valide pour son adresse : au moment de la vérification, la racine obtenue ne serait pas la même que celle du smart-contract.
Conclusion
L'arbre de Merkle est une structure de données très utile et nous n'avons pas évoqué tous les cas d'usages possibles ! Bien qu'assez ancienne, elle est toujours d'actualité et très largement utilisée dans l'univers des crypto-monnaies.
Cela fait partie des concepts fondamentaux de la blockchain à connaître, surtout si vous êtes développeur web3 car c'est devenu la norme pour construire une whitelist dans un projet NFT.
Bibliographie
[1] R. C. Merkle, “A Digital Signature Based on a Conventional Encryption Function,” in Advances in Cryptology — CRYPTO ’87, Berlin, Heidelberg, 1988, pp. 369–378.
[2] S. Nakamoto, “Bitcoin: A Peer-to-Peer Electronic Cash System,” p. 5, 2009.
[3] “Ethereum Developer Bootcamp — Merkle Trees,” Alchemy University, 2023.
